Learning From Trajectories
NOTE
This post contains a potentially publishable idea in machine learning. I cannot pursue it due to time constraints. But if you do, please link to this post, or even better, drop me short email. Maybe then I have more free time to investigate this. If you are aware of a publication with similar idea, please also let me know. I can then remove this note and cite them here. Thanks!
In computational neuroscience, it is widely accepted that the momentary state of neurons \(X(t)\) represent the task they are ought to performed. Whether its classifying a previously shown stimlus into a few categories, memorizing it, or predicting what comes next. A goal of the downstream set of neurons is to see that and transform this state \(X(t)\) to that useful target computation \(y\). The key, however, is that the computation must be embedded in the instanteneous state. But in reality, the downsteam neurons are not merely some memoryless machines that map \(X(t)\) to \(y\). I suspect that is just a computational simplification. The downstream neurons integrate whatever they see from \(X(t)\), and maintain a trace of it, and potentially compute not just using the momentary input \(X(t)\), but also its (recent) past.
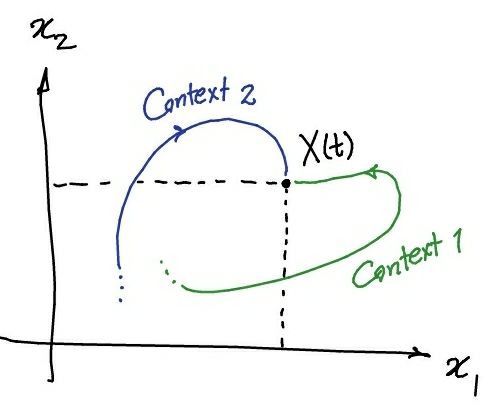
Think about a simple system that has only two neurons, whose momentary rates can be shown as a point in the 2D plane. You are the downstream system which has to infer the state to do computation. Let’s say at time \(t\), system is at state \(X(t) = (x_1(t), x_2(t))\). But now, assume, in addition to the state, you have access to some memory of the history of \(X\), i.e., its trajectory. Obviously now you can do more computation inputs can be separated based on their trajectories as well. Simply put, now, not only you care about the state, but aslo how that state was realized. This naturally gives you the ability to form a context-dependent computaiton.
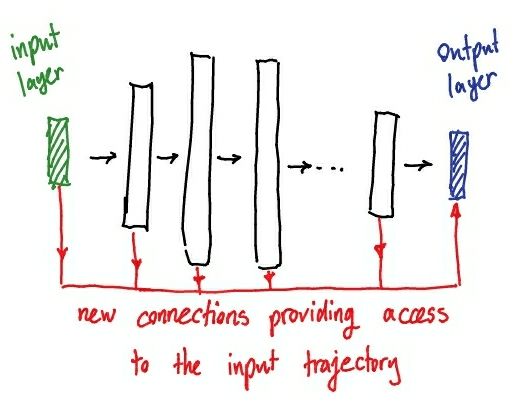
This might seem trivial in the world of recurrent neural networks (RNN). But what about deep neural nets (DNN)? In fact, DNNs, too, leverage from the trajectory, sort of. Let’s first clarify the concept of time in DNN. Time, at best, is only present through the index of the layer that is processing the input. As the input goes through each layer, it transforms, in the same way it evolves in time in the case of RNNs. Now, what if we garrant the last layer, the readout, access to the intermediate transformations of the input, i.e., its “temporal trajectory”? Then, the last layer will know how exactly an input is transformed, step by step, to give raise to that last activation map. These are exactly the skip connections, or skip pathways U-net architecture, for instance.
I have highlight that this idea stresses mainly on the importance of the last layer. This is not typical in skip connections (as we see the in residual nets). My gut feeling says that this architecture helps a lot to alleviate adversarial attacks since it can track the evolution of the input and potentially figure out something is not right in the evolution trajectory. Would be very nice to try it out and see if that its really the case or not.